728x90
[문제 링크] boj 11053 가장 긴 증가하는 부분 수열 자바 풀이
https://www.acmicpc.net/problem/11053
11053번: 가장 긴 증가하는 부분 수열
수열 A가 주어졌을 때, 가장 긴 증가하는 부분 수열을 구하는 프로그램을 작성하시오. 예를 들어, 수열 A = {10, 20, 10, 30, 20, 50} 인 경우에 가장 긴 증가하는 부분 수열은 A = {10, 20, 10, 30, 20, 50} 이
www.acmicpc.net
[생각 흐름]
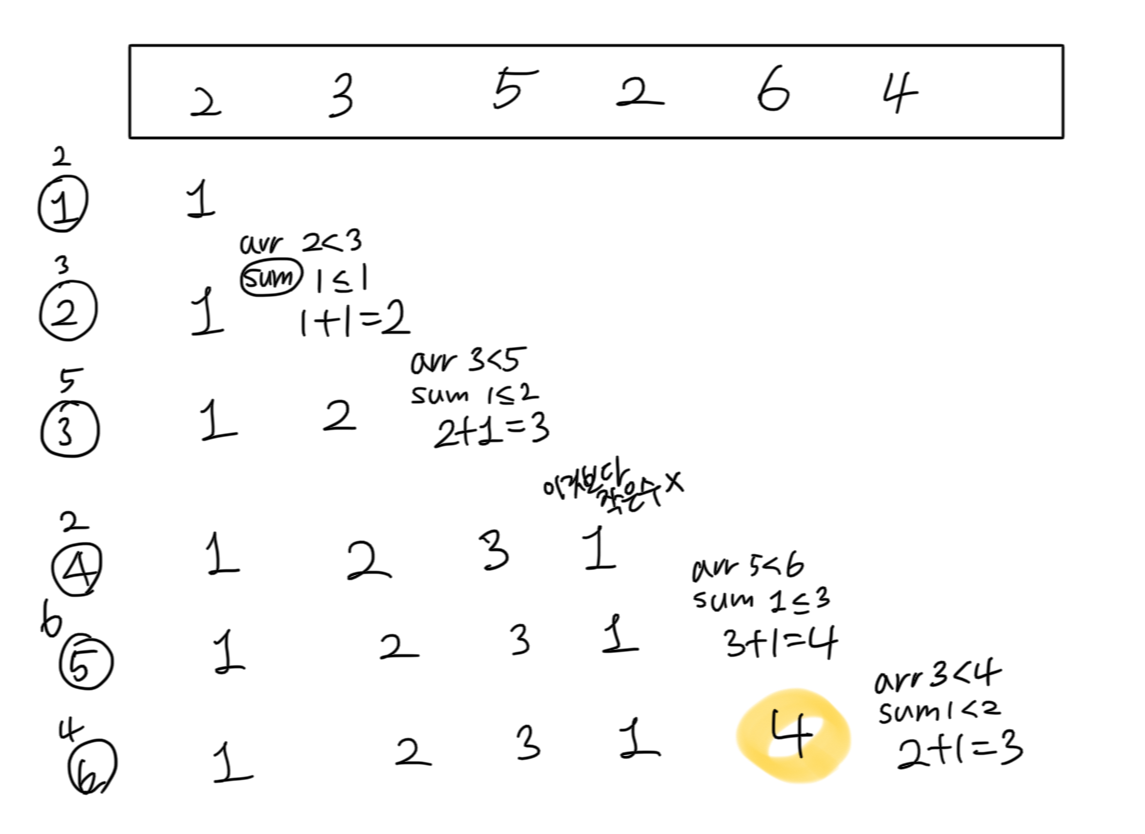
dp(다이나믹 프로그래밍)을 이용하여 문제를 해결했다.
앞에서부터 arr[i]를 포함한다는 전제로(일종의 기준점)
arr[i]보다 작고(arr[i]보다 작아야 arr[i]가 커서 증가하는 부분 수열 이므로)
sum[j]( 0~j까지의 최대 증가 부분 수열)이 sum [i] (0~i까지의 최대 증가 부분 수열) 보다 크다면 sum[i] = sum[j]+1 과 같은 방법으로 앞에서부터 뒤로 증가하는 부분 수열을 계산하였다. (sum[i]에는 갱신되면서 max 부분 수열의 길이가 저장된다)

[코드]
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
StringTokenizer st;
int numberCount = Integer.parseInt(br.readLine());
st = new StringTokenizer(br.readLine());
int arr[] = new int[numberCount];
int sum[] = new int[numberCount];
for(int i=0;i<numberCount;i++){
arr[i] = Integer.parseInt(st.nextToken());
}
for(int i=0;i<numberCount;i++){
sum[i]=1;
for(int j=0;j<i;j++)
if(arr[i]>arr[j] && sum[i]<=sum[j])sum[i] = sum[j]+1;
}
int max = 0;
for(int i=0;i<numberCount;i++)
max = Math.max(sum[i],max);
System.out.println(max);
}
}728x90
'알고리즘' 카테고리의 다른 글
| [백준 JAVA]1806 부분합 (1) | 2022.10.07 |
|---|---|
| [백준 JAVA] 2239 스도쿠 풀이 (0) | 2022.10.05 |
| [백준 JAVA]14502_연구소 (1) | 2022.09.29 |
| [백준] 14938_서강그라운드_플로이드 워셜 (0) | 2022.09.28 |
| [백준]12851_숨바꼭질 2 (0) | 2022.09.28 |


댓글